『三国志』に描かれている時代といえば、儒教が重んじられていたイメージが強く、経書の内容さえ理解していれば無双できる文系にとって天国のような時代だったように思えますが、決してそんなことはありませんでした。役人を志す場合、一般教養レベルの数学の知識を身につけていることは必須条件。義務教育として習う小学校・中学校の算数・数学レベルの計算くらいはホイホイ解けなければ地方の木っ端役人にもなれませんでした。
計算をするときの強い味方・算木
複雑な計算の場合、その過程を分解して問題を解きます。ところが、その過程を正確に記憶したり整理したりというのは至難の業。というわけで、私たちは紙に計算の過程をメモして筆算をします。しかし、三国時代には計算式をメモするために紙を使うなんていう贅沢はできませんでした。また、彼らは普段竹の札に文字を書いていましたが、この細い竹の札に計算式をズラズラ書きつけても、途中でバラバラになってしまい、結局過程がわからなくなってしまう危険性が高いでしょう。
では、彼らはどのように計算をしていたのでしょうか?…まさか頭の中で!?いえいえ、流石の彼らにもそれは厳しかったことでしょう。三国時代の人々は「算木」というものを使って計算問題を解いていたのです。
算木ってどんなもの?
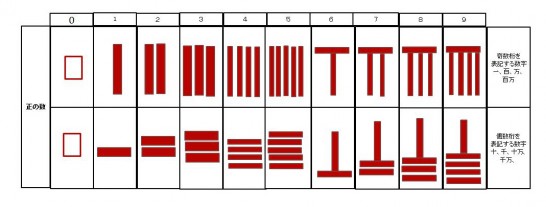
算木の見た目は、イメージとしては小学校の算数セットに入っている計算棒に近いです。長さは色々あったようですが、1セットの中に入っているものは全て同じ長さで、細長い直方体の棒だったようです。その素材は竹や木のことが多く、色は赤と黒の二種類に塗り分けられていました。赤は正の数を、黒は負の数を指すということで、今の中学一年生レベル以上の計算をするであろうことが前提として作られているのです。
算木を並べて数を表す
では、この同じ長さの細い棒を使ってどのように数を表すのでしょうか?まず、1~5までは簡単です。ただその数と同じ本数の算木を並べてあげるだけでOK。問題は6~9。6~9は5を表す横棒の下に、その数字から5を引いた数の分の算木を並べて示します。ちょっとローマ数字と似ていますよね。
10以上の数字はどうやるの?
9まではおさえられましたが、10以上の数を表すにはどうすれば良いのでしょうか?
二桁以上の数字については、その位ごとに算木を並べてあげればいいのです。ではさっそく10をつくってみたいのですが、ここで一つ問題が発生します。0がないのです。三国時代には0という概念はあっても、0を示す方法がありませんでした。というわけでまず、第一位(一の位)は空白として間をあけておくことになります。続いて第二位(十の位)ですが、第一位の左に算木を並べます。
このとき注意しなければならない点が1つ。偶数桁については、算木を並べる向きを変えなければならないのです。1~5については90度回転させ、6~9については、上にある5を表す棒を縦にして、下にある縦にしていた棒を横にするのです。このように、奇数桁と偶数桁で算木の向きを変えることにより、数字を読み取りやすいようにしているのだそうです。というわけで、10をつくる場合には、左に漢数字の「一」のように算木をおき、右側を少し空けておけばOKです。
レッツ!算木で計算!
算木の基礎をおさえたところで、さっそく算木を使って計算してみましょう。12小学校の算数セットがお手元にあるという人は、それを引っ張り出して計算してみましょう。
「7034+283」
まずは算木を使って「7034」と「283」を作りましょう。「7034」は奇数桁の第一位には縦に4本、偶数桁の第二位には横に3本、奇数桁の第三位(百の位)は空白にして、偶数桁の第四位(千の位)には上に縦1本とその下に横に2本、算木を並べてあげれば完成です。
続いてその下に「7034」と位を合わせて「283」を作りましょう。第一位には縦に3本、第二位には横に1本とその下に縦3本、そして第三位には縦2本の算木を並べてあげればOKです。次はいよいよ計算ですよ。算木での計算は、我々が小学校で習う足し算の筆算の要領と同じです。最初に計算するのは第一位。すなわち、「4+3」をすればいいのです。4+3=7ですから、横1本の下に縦2本算木を並べてあげましょう。
続いて第二位は3+8=11となり、繰り上がりの手続きをしなければなりません。その場合、第三位の上あたり算木1本を移動しておき、算木で一本を横にして置いて、残った1をつくってあげましょう。第三位は繰り上がってきたものをあわせて1+0+2=3となります。奇数桁なので算木を縦に3本並べます。最後の第四位は7しかありませんから、そのまま下ろしてあげればOKです。
三国志ライターchopsticksの独り言
解けましたか?まだまだ色々な計算ができるという算木。皆さんも算木を使って色々な計算に挑戦してみましょう!
▼こちらもどうぞ
【はじめての孫子】第6回:勝つために最も大切なことは智謀でも勇気でもなく、緻密な計算